[Deep Learniong from Scratch 1] chap.6 학습관련 기술들 part 2

4 minute read

Deep Learning from Scratch | chap.6 학습관련 기술들 - part2

이전 내용 :

위 이미지는 활성화 함수로 ReLU 를 사용했을 때, 도출되는 활성화 값이다.

위에서부터

표준편차가 0.01인 정규분포를 가지는 가중치
Xavier 초깃값 ( 표준편차 = 1/sqrt(n) )
He 초깃값 ( 표준편차 = sqrt(2/n) )

ReLU 에 가장 최적화 된 초깃값은 He 초깃값이기 때문에 치우치지 않고 균일하게 분포하는 것을 확인할 수 있다.

6.2.4 MNIST 데이터셋으로 본 가중치 초깃값 비교

위 그래프는 activation function으로 ReLU를 사용한 신경망에 ‘실제’데이터(MNIST)에 대하여 초깃값별 성능에 영향을 끼치는 것을 실험한 그래프이다.

1. std=0.01 인 경우 기울기 소실 발생
2. He, Xavier의 경우 정상적으로 학습됨

6.3 배치 정규화

각 층에서의 활성화값이 적당히 분포되도록 조정하는 것

6.3.1 배치 정규화 알고리즘

배치 정규화의 효과
1. 학습을 빨리 진행할 수 있다.(학습 속도 개선)
2. 초깃값에 크게 의존하지 않는다.
3. 오버피팅을 억제한다. (드롭아웃 등의 필요성 감소)

배치 정규화는 미니배치 단위로 행렬곱 이후에 activation function의 앞 뒤에서 실행된다.

배치 정규화는 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화 하는 작업입니다. ( 미니배치 B={x_1,x_2,…… , x_m} )

epsilon은 0으로 나눠지는 것을 막기위한 수치적 안정성을 보장하기 위한 작은 값. gamma는 scale(확대) 에 대한 값이고 beta는 sift(이동) 에 대한 값이다.

데이터를 계쏙 정규화 하게 되면 활성화 함수의 비선형 같은 성질을 잃게 되는데 이러한 문제를 배치 정규화를 이용하여 완화할 수 있다.

이러한 계산을 통해 흐르는 활성화 값들이 적절한 분포를 가지게 되어 한쪽으로 치우치는 것을 방지한다.

6.3.2 배치 정규화의 효과

아래 그림은 MNIST 데이터셋에 대하여 표준편차를 바꿔보며 배치 정규화의 효과를 실험한 그래프이다.

확인할 수 있듯이 대부분의 경우에서 배치 정규화를 이용한 경우에 더욱 성능이 좋아지는 것을 확인할 수 있다. 가장 아래 그래프의 경우에서는 표준편차가 너무 작기 때문에 배치 정규화를 진행하지 않았을 경우에 gradient vanishing이 발생하는 것을 확인할 수 있다.

6.4 바른 학습을 위한 여러가지

Overfitting : train 데이터에 지나치게 적응되어 test데이터셋에 대한 성능이 낮아지는 상태

범용성 확보를 위해 꼭 극복해야 하는 과제!!

6.4.1 Overfitting

오버피팅이 일어나는 경우
1. 매개변수가 많고 표현력이 높은 모델
2. 훈련 데이터가 적음

아래 코드는 오버피팅이 발생하는 상황을 인위적으로 만들어 학습시키는 코드이다.

훈련데이터 중 300개만 사용 - 훈련데이터의 갯수 적음
7층 네트워크 사용 - 매개변수 많음 ( 모델이 복잡함 )

# coding: utf-8
import os
import sys

sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 오버피팅을 재현하기 위해 학습 데이터 수를 줄임
x_train = x_train[:300]
t_train = t_train[:300]


network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = SGD(lr=0.01) # 학습률이 0.01인 SGD로 매개변수 갱신

max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0

for i in range(1000000000):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grads = network.gradient(x_batch, t_batch)
    optimizer.update(network.params, grads)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)

        epoch_cnt += 1
        if epoch_cnt >= max_epochs:
            break

위 코드를 통해 도출되는 accuracy는 다음과 같다.

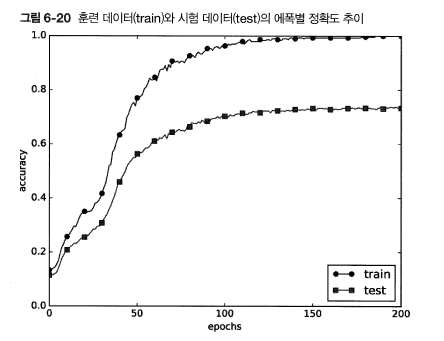
그래프를 통해 확인할 수 있듯이 train data에 대해서는 꾸준히 정확도가 올라가지만 test data에 대해서는 어느정도 정확도가 올라가다가 특정 지점에서 상승률이 더뎌진다.

6.4.2 가중치 감소

오버피팅을 방지하는 여러 방법중 가중치 감소(weight decay)가 있다.

가중치 감소(Regularization) : 학습에서 발생하는 에러말고, 평가를 위한 테스트상에서 발생하는 에러(generalization error)를 줄이기 위하여 학습 알고리즘을 수정하는 기법

가중치의 값에 L2 norm을 적용시켜 Loss값에 더해준다.

이러한 방식은 큰 가중치에 대해서 큰 만큼 가중치의 값을 감소시키게 한다. (Loss 값이 커지면 즉, 가중치의 값이 커지면 오차역전파를 통해 구해진 gradient값이 커지기 때문에 가중치가 지나치게 커지는 것을 막을 수 있다. )

위 그래프는 가중치 감소를 적용한 모델의 성능을 나타낸 그래프이다. 적용하지 않았을 때 보다 test데이터에 대해서 성능이 좋아진 것을 확인할 수 있다. (오버피팅이 억제됨)

6.4.3 드롭아웃

신경망 구조가 너무 복잡해진다면(가중치의 수가 지나치게 많아지면) 가중치 감소의 방법으로는 어느정도 한계가 있을 수 있다.

또 다른 overfitting을 방지하기 위한 방법으로 드롭아웃이 있다.

드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법이다.

훈련 때 은닉층의 뉴런을 무작위로 골라 삭제한 채로 학습을 시키게 되고, 테스트 때는 모든 뉴런을 활성화 한 채로 값을 전달하게 된다. ( 각 뉴런의 출력에 훈련 때 삭제한 비율을 곱하여 출력 )

결과 :

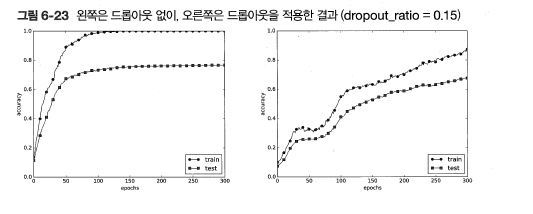
위 그래프에서 확인할 수 있듯이 학습속도는 줄어들지만 train dataset과 test dataset과의 격차가 줄어들었다. 따라서 overfitting을 억제하는데 효과적이라는 것을 알 수 있다.

6.5 적절한 하이퍼파라미터 값 찾기

하이퍼파라미터는 모델에 대해서 직접 설정해 주어야 하는 매개변수를 의미한다. 이러한 하이퍼파라미터는 일반적으로 많은 시행착오를 겪는 방식으로 최적의 하이퍼 파라미터를 찾아야 하고 모델의 성능에 큰 영향을 미친다.

6.5.1 검증 데이터

우리는 데이터셋을 train, validataion, test dataset으로 나눈다. train dataset은 단순히 학습을 위한 dataset이고 validation dataset은 train dataset을 기반으로 학습된 모델의 성능을 평가하기 위한 dataset이고 test dataset은 최종적으로 모델의 범용성을 확인하는 dataset이다.

validation dataset을 기반으로 하이퍼파라미터를 설정함으로써 test dataset에 대한 오버피팅을 방지할 수 있다.

아래 코드는 데이터셋에서 validation dataset을 분리하는 코드이다.

6.5.2 하이퍼파라미터 최적화

하이퍼파라미터를 최적화 하는 핵심 아이디어는 최적 값이 존재하는 범위를 조금씩 줄여가는 것이다.

grid search : 정해진 범위 내에서 정해진 간격만큼 이동하며 hyper parameter를 적용 random search : 정해진 범위 내에서 랜덤한 간격으로 hyper parameter 적용

전체 학습을 여러번 반복하여 탐색하기 때문에 학습시간이 굉장히 오래 걸린다.

적용 순서

하이퍼파라미터 값의 범위를 설정
설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출
1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고 검증데이터로 정확도 평가
1단계와 2단계를 특정 횟수 반복하여, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힘

6.5.3 하이퍼파라미터 최적화 구현

위에서 알아본 random search방식을 이용해 MNIST 데이터셋에 대한 모델의 가중치 감소의 세기와 학습률을 조절해 본다.

# random.uniform(a,b) : 두 실수 사이의 랜덤 실수 생성( a <= x <b )
weight_decay = 10 ** np.random.uniform(-8,-4)  
lr = 10 ** np.random.uniform( -6,-2)

결과 :

best-5 까지 학습이 원할하게 진행되는 것을 확인할 수 있다. 이러한 방식으로 최적의 hyper parameter값의 범위를 좁혀가며 심험해야 한다.

끗!

Twitter Facebook LinkedIn

Seok-Jong