[CS231n] Lecture 4

[CS231n] Lecture 4 | Introduction to Neural Networks

## 1. Gradient (Backpropagation)

이전 강의에서 optimization에 대해 간략히 알아보았다. 이번에는 각각의 가중치에 대한 gradient를 어떻게 도출하는지 computational graphs로 알아본다.

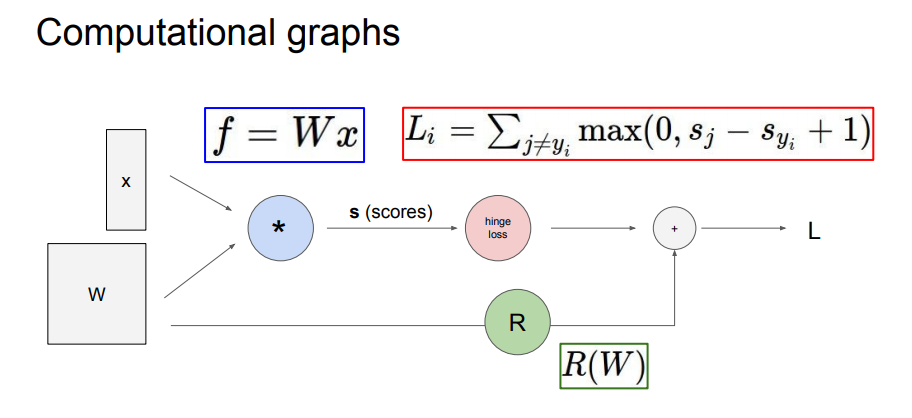
Computational graphs는 위 이미지와 같이 계산 방식을 노드를 통해 표현하는 방식으로 graphs 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용함으로써 backpropagation을 수행한다.

backpropagation의 계산 방식에 대해서 가볍게 정리하고 넘어가겠다.

위 그래프를 보면 초록색으로 표시된 숫자가 순전파의 경우에 전달되는 값이고 빨간색으로 표시된 숫자가 역전파의 경우에 전달되는 값이다.

먼저 우리가 역전파를 통해서 얻고자 하는것이 무엇인지 파악할 필요가 있다.

이전 강의에서 배웠듯이 경사하강법을 통해 loss값을 줄이기 위해서는 최종 loss값에 대한 가중치의 변화량을 조사하여야 한다. 역전파방법을 통해 도출된 값은 최종 loss에 대해 해당 값이 가지는 변화량을 의미하며 이 변화량에 -lr(learning rate)를 곱하여 가중치에 더하게 된다. lr값으로는 보통 0.01에서 0.001의 값을 할당하며 작은 변화량을 여러번 적용시켜 loss가 최소가 되는 지점에 점진적으로 도달하는 것이 목표이다.

그렇다면 각각의 w값이 loss에 미치는 영향을 알아야 하는데 이것을 구하는 방법이 바로 backpropagation이라고 할 수 있다.

기본적으로 최종값에 대한 각각의 원소를 구하는 방법은 chain rule이라는 규칙을 따라서 계산된다. 이전 강의에서 미분을 통해 가중치 변화량에 대한 loss값 변화량에 대해서 알아봤는데 computational graphs에서도 똑같이 적용된다. 다만 어러 노드들을 거침으로써 우리는 부분적인 변화량을 계산하여야 하는데 이러한 과정에서 합성함수의 미분 개념이 도입되게 되고 이러한 것이 반복적(재귀적)으로 적용하는 것이 바로 chain rule이다.

우리가 구하길 원하는 loss값 변화량에 대한 w값 변화량은 downstream gradient 인데 이는 local gradient x upstream gradient이다.

계산 방식에 대한 자세한 내용은 강의를 참고하여 이해하는 것이 좋다.

실제로 backpropagation에 흐르는 데이터들은 scala값이 아니라 vector값으로 흐르게 된다. vector값으로 흐르게 되는 경우에도 계산 방식은 같다고 볼 수 있다. 다만 순전파떄와 역전파때의 shape이 같아야 하기 때문에 Transpose를 적용해야 한다는 점을 유념해야 한다.

이러한 계산방식에 대해서 전부 이해할 수 있다면 물론 좋곘지만 이해가 어렵다면 전체적인 흐름의 원리만 파악한다고 해도 좋을 것 같다. 우리가 흔히 사용하는 tensorflow나 keras , pytorch 등의 딥러닝 프레임워크는 간단한 method를 통해 이러한 복잡한 과정을 손쉽게 수행해 준다. 하지만 보다 깊은 이해를 위해서는 딥러닝 프레임워크를 사용하지않고 직접 모델을 만들어 보면서 내용을 익히는 것이 큰 도움이 될 거라고 생각한다.

2. Neural Networks

이번에는 Neural Networks에 대해서 알아본다.

우리는 데이터에 대해서 원하는 수행을 해내는 모델을 만들어야 한다. 이 모델은 기본적으로 입력된 train dataset을 통하여 학습하는데 단 하나의 층을 가진 모델은 데이터를 깊게 들여다 보지 못한다. 따라서 층을 여러개 쌓아 데이터에 존재하는 feature들을 이해하고 그것들을 바탕으로 가중치를 업데이트하며 최종적으로 test dataset에 대해서 원하는 결과를 도출하는 성능 좋은 모델을 만들어야 한다.

이전에 우리는 templete을 통해서 가중치가 어떠한 방향으로 업데이트 되는지 알아보았다. 그때 살펴본 templete은 위 이미지에서 w1에 해당하는 가중치를 이미지의 shape로 바꾸어 재구성한 모습이다. 행렬곱의 특성상 input image와 값이 같아져야 더 높은 score를 배출하기 떄문에 가중치가 점점 input data의 형태로 바뀜을 확인할 수 있다. 여기서 살펴본 templete은 가장 낮은 층의 가중치를 이용했다는 것에 주목해야 한다. 낮은 층의 가중치는 input image와 가장 전체적인 연관성이 높다고 볼 수 있다. 왜냐하면 순수한 input image와의 연산을 수행하기 때문이다. 하지만 층이 깊어질수록 깊은 층의 w들을 시각화 한다면 이는 더 이상 사람이 이해할 수 없는 형태의 이미지일 것이다. 왜냐하면 층이 깊어질수록 input data에 대한 보다 심오한 feature에 주목하기 때문이다.

이것이 무엇을 의미하는지는 정의하기가 어렵다. 예를들어 이미지에 대한 선과 선사이의 관계나 채도와 채도와의 관계를 나타낼수도 있다. 하지만 명백하게 w가 무엇을 의미한다고 정의할 수 없고 그저 이미지가 가지고 있고 인간이 이해할 수 없는 심오한 데이터(데이터와 데이터의 관계)를 의미하고 있다고 한다.

결론적으로 성능이 좋은 모델을 만드려면 모델의 신경망은 어느정도의 깊이를 확보하고 있어야 한다.

CF) 이러한 신경망의 깊이는 모델의 복잡도를 의미하는데 데이터의 분산과 편향을 고려하여 신경망의 복잡도를 조절할 필요가 있다. 참고 - https://opentutorials.org/module/3653/22071

Reference

https://www.youtube.com/watch?v=d14TUNcbn1k&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=4

http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf

https://opentutorials.org/module/3653/22071

https://brunch.co.kr/@gimmesilver/44